One of the mysteries of Mathematics seems to be the concept of "infinity", usually denoted by the symbol 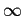 . So what is
. So what is 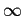 ? It is simply a symbol that represents large numbers. Indeed, numbers are of three kinds: large, normal size, and small. The normal size numbers are the ones that we have a clear feeling for. For example, what does a trillion mean? That is a very large number. Also numbers involved in macro-physics are very large numbers. Small numbers are usually used in micro-physics. Numbers like 10-75 are very small. Being positive or negative has special meaning depending on the problem at hand. The common mistake is to say that
? It is simply a symbol that represents large numbers. Indeed, numbers are of three kinds: large, normal size, and small. The normal size numbers are the ones that we have a clear feeling for. For example, what does a trillion mean? That is a very large number. Also numbers involved in macro-physics are very large numbers. Small numbers are usually used in micro-physics. Numbers like 10-75 are very small. Being positive or negative has special meaning depending on the problem at hand. The common mistake is to say that  is smaller than 0. While this may be true according to the natural order on the real line in term of sizes,
is smaller than 0. While this may be true according to the natural order on the real line in term of sizes,  is big, very big!
is big, very big!
So when do we have to deal with 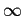 and
and  ? Easy: whenever you take the inverse of small numbers, you generate large numbers and vice-versa. Mathematically we can write this as:
? Easy: whenever you take the inverse of small numbers, you generate large numbers and vice-versa. Mathematically we can write this as:
Note that the inverse of a small number is a large number. So size-wise there is no problem. But we have to be careful about the positive or negative sign. We have to make sure we know whether a small number is positive or negative. 0+ represents small positive numbers while 0- represents small negative numbers. (Similarly, we will use e.g. 3+ to denote numbers slightly bigger than 3, and 3- to denote numbers slightly smaller than 3.) In other words, being more precise we have
Remark. Do not treat 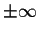 as ordinary numbers. These symbols do not obey the usual rules of arithmetic, for instance,
as ordinary numbers. These symbols do not obey the usual rules of arithmetic, for instance, 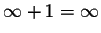 ,
, 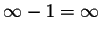 ,
, 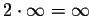 , etc.
, etc.
Example. Consider the function
When

, then

. So
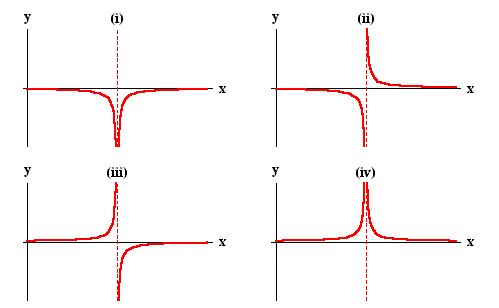
Note that when x gets closer to 3, then the points on the graph get closer to the (dashed) vertical line x=3. Such a line is called a vertical asymptote. For a given function f(x), there are four cases, in which vertical asymptotes can present themselves:
- (i)
-
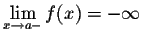 ;
; 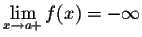 ;
; - (ii)
-
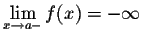 ;
; 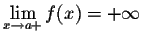 ;
; - (iii)
-
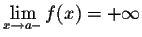 ;
; 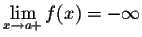 ;
; - (iv)
-
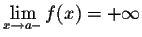 ;
; 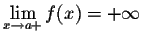 ;
;
Next we investigate the behavior of functions when 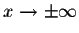 . We have seen that
. We have seen that 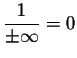 . So for example, we have
. So for example, we have
In the next example, we show how this result is very useful.
Example. Consider the function
We have
which implies
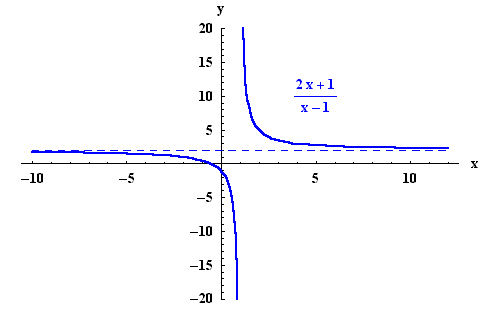
Note that when x gets closer to 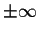 (x gets large), then the points on the graph get closer to the horizontal line y=2. Such a line is called a horizontal asymptote.
(x gets large), then the points on the graph get closer to the horizontal line y=2. Such a line is called a horizontal asymptote.
In particular, we have
for any number
a, and any positive number
r, provided
xr is defined. We also have
For

, we have to be careful about the definition of the power of negative numbers. In particular, we have
for any natural number
n.
Example. Consider the function
We have
So we have
Example. Consider the function
We have
and then
When
x goes to

, then
x > 0, which implies that |
x| =
x. Hence
When
x goes to

, then
x <>x| = -
x. Hence
Remark. Be careful! A common mistake is to assume that 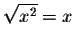 . This is true if
. This is true if 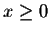 and false if x <>
and false if x <>






![]() and
and ![]() ? Easy: whenever you take the inverse of small numbers, you generate large numbers and vice-versa. Mathematically we can write this as:
? Easy: whenever you take the inverse of small numbers, you generate large numbers and vice-versa. Mathematically we can write this as:
![]() as ordinary numbers. These symbols do not obey the usual rules of arithmetic, for instance,
as ordinary numbers. These symbols do not obey the usual rules of arithmetic, for instance, ![]() ,
, ![]() ,
, ![]() , etc.
, etc. 
![]() . We have seen that
. We have seen that 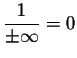 . So for example, we have
. So for example, we have
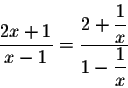
![]() (x gets large), then the points on the graph get closer to the horizontal line y=2. Such a line is called a horizontal asymptote.
(x gets large), then the points on the graph get closer to the horizontal line y=2. Such a line is called a horizontal asymptote. 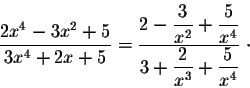
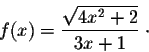
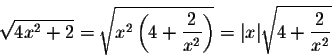
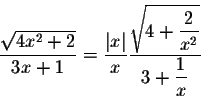
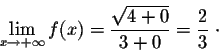
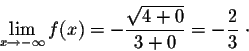
![]() . This is true if
. This is true if ![]() and false if x <>
and false if x <>